Kamatos kamatszámítás képlete

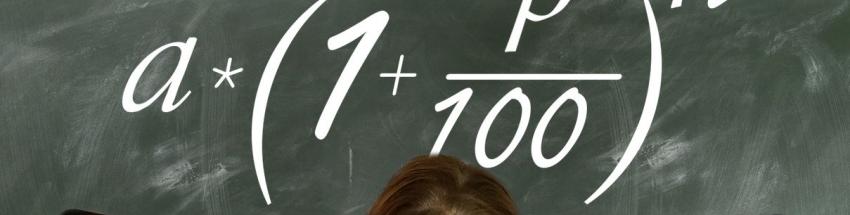
Kamatos kamatszámítás képlete kissé bonyolultnak tűnik, de elemezzük, nézzük csak meg miről is van szó:

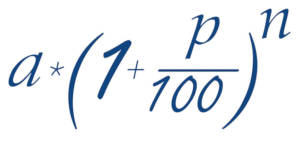
Számíthatjuk excel táblázatban, kalkulátorral, online kalkulátorral - a számítás alapja ez a képlet. A képlet eredménye egy a induló alaptőke(kezdő tőke), n kamatszámítási periódus(futamidő) alatt, p kamatos kamatlábbal növelt értéke. Ez azt jelenti:

• a képlet baloldalán a jé jövőérték áll, azaz a kamatos kamat képlete a n futamidő végén, az a induló tőke és p kamatláb értékével, a jövőértéket fejezi ki;
• az induló a alaptőke a kamatszámítás periódusainak végén tovább nő, a kamat értékével, azaz a kamat is kamatozni fog a továbbiakban. Ezzel nő a kamatszámítás induló vagy kezdőtőkéje;
• a kamatfizetési periódus végén, amikor megtörténik a kamat kiszámítása és azt hozzáadják a kamatozó összeghez, ezt tőkésítésnek is nevezik.
• kamatos kamatszámításnál minden kamatfizetési periódus végén megtörténik a tőkésítés;
• az n kamatszámítási periódust - futamidőt - megadhatjuk hónapokban vagy években - elméletileg bármilyen idő egységben. A periódus az az egység, amelyre a kamatláb adott;
• a képlet kitevőjében lévő n érték a kamatszámítási periódusok mennyisége, azaz pl.:  az évek vagy hónapok száma;

A kamatos kamatszámítás képlete alkalmas arra, hogy a számítás bármely összetevőjét - matematika szabályai alapján - kifejezzünk. Ez teszi lehetővé, hogy a 4 paraméter bármelyikét ki tudjuk számolni vele, a 3 ismeretében.

A videóban x-el jelöli a forrás GevaPC Tudástár a kamatos kamatszámítás képletében a kezdő tőkét vagy másként megfogalmazva a jelenértéket. Minden más jelölés egyezik jelen Számítások webhely jelölésével.

Kamatos kamat képlete, most kamatos kamatláb számításához

A fenti képlettel a kamatos kamat jövőértékét számíthatjuk ki. A kamatos kamatláb számításához a lábat először ki kellene fejeznünk a képletből.

Kifejezni egy változót a képletből, annyit tesz, hogy úgy hajtunk végre matematikai műveleteket - összeadás, kivonás, szorzás, osztás, ... - az egyenletünk mindkét oldalával, hogy az egyik oldalon a kívánt változó maradjon. Matematikai tanulmányaidból felderenghet a kifejezés értelme. Ennek a műveletsornak az a lényege, hogy bármilyen matematikai műveletet is végzünk, az egyenlet mindkét oldalával, az egyenlőség fennmarad, mert az egyenlőségnek fenn kell maradnia!

Ha kifejeztük a kamatlábat, azaz a kamatláb változója a p lesz az egyenlet egyik oldalán a matematikai műveleteknek köszönhetően, akkor már ki tudjuk számolni azt, a futamidő, az indulótőke és a jövőérték ismeretében.

A kamatos kamat láb kifejezéséhez a kiindulásnál:

• az egyenlet egyik oldalán van a jövőérték változója;
• az egyenlet másik oldalán van egy hosszabb képlet, amelyben a p a kamatlábat képviseli, ezt kellene kifejeznünk az egyenletből;
• a matematikai műveletekkel kívülről-befelé haladva hajtjuk végre. Azzal a művelettel indítunk, amelyet a képletünkben utoljára kellett végrehajtani, pontosabban annak az ellentétes műveletével. Ha a képletben pl összeadás az utoljára elvégzett művelet, akkor kivonással kezdünk: a képletben hozzáadott értéket vonjuk le az egyenlet mindkét oldalából.
  A kamatos kamatláb képletében az utoljára elvégzett művelet a szorzás volt, ezért osztanunk kell az egyenlet mindkét oldalát a a változóval.

hamarosan elkészítem azt a lépésről-lépésre írást, amelyben kifejezem a kamatos kamat számítás képletéből a kamat lábat, belinkelem a kapcsolódó írásokhoz.