A kamatszámítás képlete

A kamatszámítás képlete alapján meghatározzuk a kamat összegét és a kamatlábat. Robot módjára számolunk és kiszámoljuk a kamatot. A képletet alkalmazhatjuk számológépen, táblázatkezelőben. Ettől akkor van csak könnyebb helyzetben, ha csak a számítás végeredménye a fontos, érteni és alkalmazni nem kell. Ez utóbbi a Számítások webhelyünk Százalék kalkulátora.

A kamatszámítás kalkulátorunknál mi is ezt a képletet alkalmazzuk a számítások elvégzéséhez, javascript nyelven kódolva.

A kamatszámítás képlete

A kamatszámítás alapja a százalékszámítás. Ha megértjük a kamatszámítást, akkor a számításokat akár a százalékszámítás kalkulátorral is elvégezhetjük.

Maradjunk most a kamatszámításnál, a terület szavaival és megfogalmazásainál.

A kamatszámítás képlet fogalmai

Alább felsoroltam a használt fogalmakat - a lexikonban is megtalálja a fogalmak és kifejezések definícióját, meghatározását - de álljon itt-, közvetlenül a képletnél a fogalmak rövid meghatározása

• Jelenérték - pénz, amellyel jelen pillanatban rendelkezik
  
  angolul Present Value, szokás ez alapján PV-vel is jelölni, pl a Magyar Nemzeti Bank is ezt használja, jelen Számítások webhelyen Je a jelölése, a jelenérték röviden(szempontom az érthetőség és nem a hivatalos, precíz képlet leírása)
• Jövőérték - pénz, amely a kamatozási idő végén rendelkezésére áll. A kamatozási idő a teljes kamatszámítás időszakát magában foglalja, azaz tartalmaz minden kamatozási periódust. Pl több évet, ha év a kamatfizetési periódus.
  
  angolul Future Value, szokás ez alapján PV-vel is jelölni, pl a Magyar Nemzeti Bank is ezt használja, jelen Számítások webhelyen Jö
• Növekedési ráta - a jelenérték növekedési mértéke, a kamatfizetési periódus végén. Egyszerű kamatszámításnál azt vesszük alapul, hogy a növekedési ráta minden periódusban azonos mértékű és kifizetésre kerül, a továbbiakban is csak az alaptőke kamatozik.
• Kamat fizetési periódusok száma - jelölése n az angol number szóból.
  
   

Jöjjön a kamatszámítás képlete!

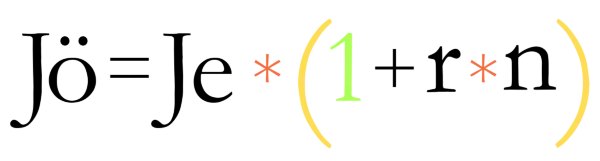
Pl.: Nézzük egy példát a jövőérték kiszámítására:

• Je = 100
• az r növekedési ráta évi 20% azaz 0,2
• n kamatfizetési periódusok száma 5 év

Jö = 100 * (1 + 0,2 * 5)  = 100 * (1 + 1) = 100 * 2 = 200

azaz a 100 jelenérték 5 év után 200 lesz. Mondhatnánk úgy is, hogy egy év után 20%-s kamattal 20 a kamat összege, 5 év alatt 5 * 20 az 100.

Mire használható a kamatszámítás képlete? Kiszámíthatók belőle:

Fentebb az alap kamatszámítás képlet látható. Ha ezzel tovább dolgozunk kicsit, akkor ezzela  képlettel kifejezhetjük, így kiszámítható vele nem csak a jövőérték, de a jelenérték, a növekedési ráta és a kamatfizetési periódusok száma is.

Jelenérték kiszámítása a kamatszámítás képlettel

A kamatszámítás képletét átalakítva - a jelenérték képlete

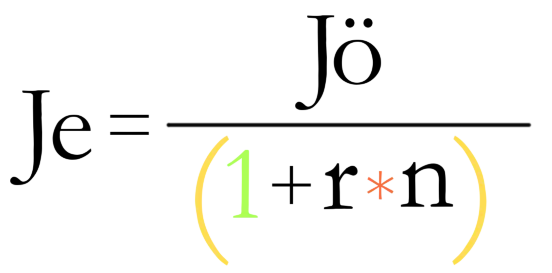
Pl.: vegyünk ismét egy példát:

• A remélt jövőérték Jö legyen 1000
• a kamatfizetési ráta r ismét 20% vagy 0,2
• 5 év kamatfizetési periódus, azaz n = 5

A feladat kérdése: Mekkora összeget kell befektetni, azaz mennyi legyen a jelenérték, ha 1000 jövőbeli értéket szeretnénk 5 év múlva, 20% növekedési rátával?

Helyettesítsük a képletbe az értékeket:

Je = 1000 / (1 + 0,2 * 5) = 1000 / 2 = 500 azaz 500-t kell jelenben befektetni, hogy 5 év múlva, 20% kamattal elérjük az 1000 jövőértéket.

Összességében a képlet használható a fenti fogalmak, kamatszámítási részletek kiszámítására.

A kamatszámítás képlete Excel-ben, táblázatkezelő munkafüzetben