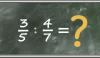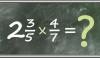Törtek, vegyes törtek összeadása

Számba vesszük a lehetőségeket, törtek és vegyes törtek összeadásához. Nem csak magyarázatra, de konkrét példára is számíthat.

Törtek és vegyes törtek

Mit is hívunk törtnek?

• Törtnek hívjuk az egynél kisebb számot, amelyet a számláló és nevező értékével fejezünk ki.
• Felül a számláló, alatta a vízszintes vonal a tört vonal,
• a törtvonal alatt a tört nevezője.
• A tört nevezője kifejezi, hogy hány képzeletbeli egyenlő részre osztjuk az egészet,
• a tört számlálója azt fejezi ki, hogy az egyenlő részekre osztott részekből hány van.

A jobbra látható tört, 3/7, azaz három heted. A számlálója 3, a nevezője 7, azaz az egészet 7 egyenlő részre osztottuk, amelyből 3 van.

A fentiekből következik:

• a számláló kisebb mint a nevezője - így lesz 1-nél kisebb
  • ha a számláló = nevezővel, akkor az 1 egésszel egyenlő; Pl.: 8/8 = 1 egész, de mind1 milyen számot írok, az eredmény mindig 1.
  • ha a számláló > mint a nevező, akkor 1-nél nagyobb :-) kifejezhető belőle az egész rész. Annyi egész, ahányszor a számlálóból kitelik a nevező.
    Pl.: 7/3 = 2 egész 1/3, hiszen a 7-ből kétszer jön ki a nevező 3, így lesz 2 egész. Ha ezt a kettő egészt, azaz a 6/7-t levonom, akkor marad 1 /3.
• a nevező nem lehet 0, hiszen a nullával való osztás nem értelmezett.

A vegyes tört egész részt is tartalmaz

Az imént mutatott tört egész része 0, azaz a 3/7 = 0 egész 3/7-l. Ez azt jelenti, hogy a 0 egészet nem szokás kiírni, egyben akkor ez egy tört is.

Valódi vegyes tört a 3 egész 2/5, a szokásos írásmódja jobbra látható.

A vegyestört tört része természetesen kisebb 1 egésznél, ha mégis nagyobb lenne, akkor ki kell belőle fejezni az egész részt, hozzáadni az egész részéhez.
Pl.: a 3 egész 9/5 vegyes törtnél a tört rész nagyobb 1 egésznél, másként kifejezve ugyanezt: a törtből kitelik egy egész, így

• a tört részből egész fejezhető ki, pontosan 1 egész = 5/5. Ezt levonjuk a tört részből és 1-t hozzáadunk az egész részhez
• az eredmény és normál vegyes tört 4 egész 4/5 lesz a 3 egész 9/5-ből.

Törtek és vegyes törtek összeadása

Több módon is elvégezhetjük az összeadást, az eredmény ugyanannyi, tehát mindegy melyikkel végezzük el a műveletet.

 Ha kettőnél több törtet kell összeadni, akkor balról jobbra haladva adunk össze 2 törtet/vegyes törtet, majd az eredmény törthöz adjuk a következő törtet/vegyes törtet.

• Az összadást mindig balról jobbra haladva adjuk össze, a sorrend tetszőlegesen állítható fel.
• A zárójel megváltoztatja ezt a sorrendet: először a záróljelen belük kell az összeadást elvégezni, ám ha minden művelet összeadás, akkor a zárójel sem változtat a végeredmény értékén.
   

A továbbiakban két vegyes tört összeadását vesszük lépésről-lépésre. Ha törteket kell összeadnunk, akkor úgy vesszük, hogy az egész rész 0, azaz nulla.

Fontos: két törtet vagy vegyes törtet akkor tudunk összeadni, ha közösnevezőre hozzuk őket.(a tört kalkulátor tartalmazza a közös nevezőre hozást is)

0. Törtek összeadásához: Közös nevezőre hozás

Keressük meg azt a legkisebb számot, amelyben mindkét összeadandó tört nevezője egész számszor meg van = közös többszörös

Pl.: ha a feladat 2/3 + 1/5 akkor a közös nevező a 15 lesz, hiszen a 3 meg van benne 5-ször, az 5 meg van benne 3-szor. Nincs ennél kisebb szám, amelyben mindkét nevező egész számszor meg lenne.
Az összeadás tehát 10/15 + 3/15 =13/15 - hiszen két azonos nevezővel rendelkező törtet úgy adunk össze, hogy összeadjuk a számlálójukat, az eredmény nevezője a közös nevező.

Ez egy egyszerű példa volt, vannak sokkal bonyolultabb számítások is :-) A közös nevező megtalálásához ajánlom a Tört kalkulátorunkat, amelyben könnyedén használható a közös nevezőre hozás is:

1. összeadás: egészet az egésszel, tört a tört résszel

Az egész részeket összeadjuk, a tört részeket összeadjuk. Ha az eredmény tört része, az összeadás hatására nagyobb lesz mint egy egész, akkor abból ki kell fejezni az egészrészt.
Pl.: 2 egész 2/3 + 1 egész 1/5

• közös nevezőre hozzuk a törteket, így alakul a feladat: 2 10/15 + 1 3/15
• összeadjuk az egész részeket = 3 egész, összeadjuk a tört részeket = 13/15 azaz 3 egész 13/15
• az eredmény törtrésze kisebb 1-nél, így ebből nem kell kifejezni az egész részt.

Bonyolultabb esetben az összeadás könnyedén elvégezhető a Tört kalkulátorunkkal, lsd lejjebb.

2. összeadás: az összeadandókat törtté alakítjuk és törteket adunk össze

Vegyük ugyanazon példát: 2 2/3 + 1 1/5

• Az egész részeket átalakítjuk törtté: 2 2/3 = (2 + 2*3)/3 = 8/3
• az 1 1/5 = (1 + 1*5)/5 = 6/5 tehát a feladat a továbbiakban 8/3 + 6/5
• közös nevezőre hozzuk:( 8 * 5)/15 + (6*3)/5 = 40/15 + 18/15 - a zárójelet akár el is hagyhattam volna, hiszen a szorzás magasabb prioritású, mint az összeadás, így mindenképpen a szorzásokat kell először elvégezni, utána az összadásokat.
• összeadjuk a számlálókat és az eredmény = 58/15
• kifejezzük az egész részt: 58-ban 3-szor van meg a 15 - 3*15 = 45, marad 13, azaz az eredmény = 3 13/15

Az előző pontnál, a kalkulátorral elvégzett összeadásnál látható is minden lépés, azaz a kalkulátor is úgy számolja ki a vegyes törtek összeadását, hogy törtté alakítja az összeadandókat, közös nevezőre hozza őket, majd összeadja a törteket. A kapott eredményből - törtből -, kifejezi az egész részt és már kész is az összadás eredménye.

Az összeadás eredményének az ellenőrzése

Az összeadandó törtekkel el kell végezni az összeadást, a Tört kalkulátorral. A teljes folyamat lépésenként követhető a kalkulátor eredmény sorában, hiszen minden rész számítás megjelenítésre kerül.