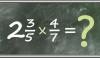Legkisebb közös többszörös számítása
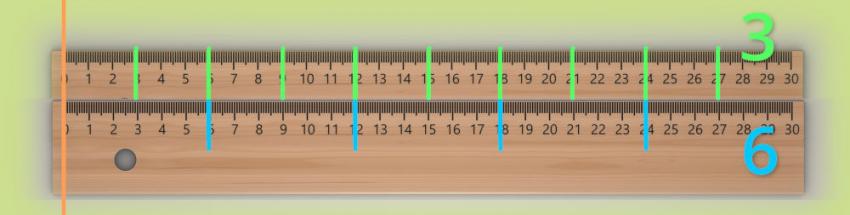
A legkisebb közös többszörösét - LKKT - számoljuk ki a 3 és a 6 számnak. A két számnak több közös többszöröse is van, ezek közül a legkisebbet - egész számot keressük. Úgy képzeljük el a lehető legegyszerűbben, ahogy a fenti képen is jelöltem:
- két vonalzót igazítottam a 0-hoz, egyiken megjelöltem az egyik szám-, a 3-s többszöröseit, a másik vonalzón a másik szám, a 6-s többszöröseit. Természetesen a sort lehetett volna folytatni, hiszen a mindkét számnak végtelen többszöröse van.
- ahol a két vonalzón jelzett többszörösök találkoznak/összeérnek, ott az a szám mindkét szám többszöröse, azaz a szám közös többszörösük.
- a létező közös többszörösök közül a legkisebbet válasszuk ki, azaz a 3 és a 6 legkisebb közös többszöröse a 6 lesz.
- ha szeretnénk a 3, 6 és 9 legkisebb közös többszörösét kiszámolni, akkor a számítást úgy kellene folytatni, hogy most a 3 és a 6 legkisebb közös többszörösének, a 6-nak és a 9-nek kell megkeresni a legkisebb többszörösét.
- két szám szorzata biztosan a két szám közös többszöröse, de nem feltétlenül a legkisebb. A példánknál maradva a 6 és a 9 -nek a szorzata 54 közös többszörösük, de létezik ennél kisebb közös többszörösük is, a 18. A 18-t osztja - maradék nélkül - a 6 is és a 9 is. 18 = 3 * 6 és 18 = 2 * 9
Két vagy több egész szám legkisebb közös többszöröse az a legkisebb egész szám, amelynek a számok mindegyike osztója. Szokás LKKT rövidítéssel is jelölni, leírni.
(Az oszthatóság alatt is azt értjük, hogy létezik olyan egész szám, amellyel maradék nélkül osztható)
Mihez számítjuk a legkisebb közös többszörös?
- Két vagy több egész szám közös többszörösét úgy számoljuk ki, hogy meghatározzuk két szám legkisebb közös többszörösét, majd a kapott eredmény véve a következő számmal keressük meg a legkisebb közös töbszöröst. Így haladunk végig, amíg elfogynak a számaink. Ez egy általános cél a számítással
- Törtek közös nevezőre hozásánál.
- Közös nevezőre hozás művelet nem változtatja meg a tört értékét, csak lehetővé tesz műveletek elvégzését a törtekkel: a tört számlálóját és nevezőjét ugyanazon számmal szorozzuk
- két vagy több törtet úgy tudunk összeadni vagy kivonni, ha az érintett törtket közös nevezőre hozzuk. Az eredményt - ahogy azt mindannyian tudjuk - közös nevezőre hozás után már csak a törtek számlálójával el kell végezni a kívánt műveletet - ez lesz az eredmény tört számlálója. A közös nevező az eredmény tört nevezője.
A közös nevezőre hozás kalkulátor segít az ellenőrzésében, a közös nevezőre hozás számításában. Ez nem más, mint az érintett törtek nevezőjének a legkisebb közös többszöröse. - Közös nevezőre hozásnál, az érintett tört számlálóját ugyanazzal a számmal kell megszorozni, amennyivel a nevezőt kellett megszorozni a közös nevezőhöz.
Legkisebb közös többszörös - számoljunk!
3 törttel egy összeadás kivonás művelet, közös nevezőre hozással. Műveletek, amelyekhez az érintett törteket közös nevezőre kell hozni, azaz meg kell határozni a nevezők legnagyobb közös többszörösét.
- A feladat: 1/3 + 5/6 - 2/9
- a közös nevező, 18
- a 3-nak és a 6-nak a legkisebb közös többszöröse a 6 - azaz az a szám, amelyet mindkét szám maradék nélkül oszt és nincs nála kisebb közös többszörös. A 6 és 9 legkisebb közös többszöröse a 18, így azt mondhatjuk, hogy a 3, 6 és 9 legkisebb közös többszöröse a 18. 18 lesz a közös nevező, a műveletek elvégzéséhez.
- az első törtnél a 3-s nevezőt 6-l kell megszoroni, hogy a közös nevezőt megkapjuk, így a számlálót is 6-l szorozzuk, hogy ne változzon az értéke. Közös nevezőre hozva az 1/3-t, 6/18 lesz.
- a második törtnél a 6 nevezőt 3-l kell megszorozni, így a számlálót is ezzel szorozzuk meg, azaz 15/18 lesz.
- a harmadik törtnél a 9 nevezőt 2-vel kell megszorozni, a számlálóját is ezzl szorozzuk meg, azaz a 2/9 -ből 4/18 lesz.
- az eredeti művelet - változatlan értékekkel, csak közös nevezőre hozva: 6/18 + 15/18 - 4/18.
- A müveleteket a számlálókkal végezzük el: 6 + 15 - 4 = 17. A törtekkel a müvelet eredménye tehát 17/18 lesz
Az eredményt ellenőrizd a Tört kalkulátor 1. sorában, balról jobbra haladva a műveletekkel: 1/3 + 5/6 = 1 1/6 . A következő lépésben a 1 1/ 6 - 0 2/9 = 17/18
(az egész mezőbe nullát írj, a kivonás műveletét a legördíthető listából válaszd ki!)
- a közös nevező, 18
- két vagy több vegyes tört esetében, az egészet átváltjuk törtté - pl a 3 egész 1/3 = 9 / 3 + 1/3, azaz 10/3 lesz. Jöhet a törtek közös nevezőre hozása, majd innéttől az előzőben leírtak szerint végezzük vele a kijelölt műveletet.
Legkisebb közös többszörös - kapcsolódó műveletek, fogalmak
A törtekkel végzett műveleteknél több kapcsolódó műveletet kell elvégeznünk. Fentebb kirajzolódik a legkisebb közös többszörös kiszámítása és célja. Tudjuk, hogy a közös nevezőre hozáshoz van szükségünk a legkisebb közös többszörös meghatározására. Mi bonyolíthatja még el a törtekkel végzett müveleteket!
- Bármely törtekkel végzett művelet eredményeként létrejöhet olyan tört, amely nagyobb 1-nél, azaz a tört számlálója nagyobb, mint a nevezője. Ekkor ki kell fejezni a törtből az egészet:
- Ahányszor ki tudjuk vonni a tört számlálójából, annyi egész az eredményben.
- A tört számláló - a kivonások utáni maradék lesz. Ha ez 0 lenne, akkor a tört csak egész részből áll, a nulla számlálóval nem írjuk ki a törtet.
- Egyszerűsítés. Erre a műveletre akkor van szükség, ha az eredmény tört számlálójának és nevezőjének van közös osztója:
- A legnagyobb közös osztóval kell osztani a tört számlálóját és a nevezőjét, az egyszerűsítéshez.
- Az egyszerűsítés a tört értékén nem változtat. Ha a tört számlálóját és nevezőjét azonos számmal szorozzuk vagy osztjuk, akkor nem változik meg az értéke.
Az egyszerűsítés műveletet ki tudod számolni a Tört egyszerűsítése kalkulátorral vagy a legnagyobb közös osztó meghatározásával
- Érdekes lehet még a prímszámok esetében hogyan alakul a legkisebb közös többszörös! Tudj meg mindent a prímszámokról - egyszerűen a ZseniMatek.hu oldalán.
- A hozzászóláshoz be kell jelentkezni